Backprop

Course

Andrej Karpathy "Hero to zero" course on nnet:

• part 1 (backprop) : https://www.youtube.com/watch?v=VMj-3S1tku0

Derivative

Definition

$$\frac{df}{dx} = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}$$

Intuition

$$\frac{df}{dx} = \text{slope of curve f(x)}$$

small change in x (h) -> small change in f

Rules

From limit definition -> derivative rules

$$\begin{align} \frac{d(k)}{dx} &= 0 \\ \frac{d(x)}{dx} &= 1 \\ \frac{d(x^2)}{dx} &= 2x \\ \frac{d(kx^n)}{dx} &= k \cdot n \cdot x^{n-1} \\ \frac{d(f(x) + g(x))}{dx} &= \frac{df(x)}{dx} + \frac{dg(x)}{dx} \\ \frac{d(f(x) g(x))}{dx} &= f(x) \frac{dg(x)}{dx} + g(x) \frac{df(x)}{dx} \\ \frac{d(e^x)}{dx} &= e^x \end{align}$$

Ex:

$$\begin{align} f(x) &= 3x^2 - 4x + 5 \\ \frac{df}{dx} &= 3 \cdot 2x - 4 + 0 = 6x - 4 \end{align}$$

Numerical approximation

if h is very small ($h \approx 0$):

$$\frac{df}{dx} \approx \frac{f(x + h) - f(x)}{h}$$

Multivariable

multiple variables -> partial derivative, assume other variables are constants.

Ex:

$$\begin{align} f(x,y,z) &= x \cdot y + z \\ \frac{\partial f}{\partial x} &= y \cdot 1 + 0 = y \\ \frac{\partial f}{\partial y} &= x \cdot 1 + 0 = x \\ \frac{\partial f}{\partial z} &= 0 + 1 = 1 \end{align}$$

$\frac{\partial f}{\partial y}$ : how does y influences f ?

small change in y when keep x,z constants -> small change in f

Autodiff / Autograd

• Automatic differentiation
• mathematical expression (function) -> graph of nodes (expression graph)
• forward pass = traverse/eval graph = eval math expression
• compute derivative of function by computing df/dV at each node using numerical differentiation

Ex:

1
2
3
4
5
6

[a] -> [+] -> [c]
[b] ->

c = a + b
dc/da = ?
dc/da = 1 + 0 = 1

impl:

1
2
3
4

Value
    Value children[2]
    operator (+, -, *, /, ^, ...)
    grad = 0 (dL/dV)

operations on : scalar (1x1), vector (Nx1), matrix(MxN), tensor(MxNxKx...)

• deriv tanh(x) -> 1-tanh(x)^2
• deriv exp(x) = exp(x) = n.value
• a / b = a * 1/b = a * b^-1
• a - b = a + (-b)

Backprop

Backpropagation = wiggle machine to figure out how inputs affect output

• backprop = reversed autodiff
• how to get output from inputs?
  • follow gradient -> chain rule
• indep of nnet

1
2
3
4
5

from end node, reverse
calc dL/dV = grad of each node, L = loss function
dL/dL = 1 (base case)
dL/dV
...

Chain rule

1

[a] -> [b] -> [L]

To find the grad of intermediate nodes (local derivative), we need to use the "chain rule":

$$\frac{dL}{da} = \frac{dL}{db} \cdot \frac{db}{da}$$

Chain rule = product rule, change or variable, convert units

Find dL/da (impact of a on L) knowing dL/b (impact of b on L) and db/da (impact of a on b).

Intuition from wiki: "If a car travels twice as fast as a bicycle and the bicycle is four times as fast as a walking man, then the car travels 2 × 4 = 8 times as fast as the man."

1
2
3
4
5
6
7
8
9

c: car
b: bike
w: walk

dc/db = 2
db/dw = 4

dc/dw = ?
dc/dw = (dc / db) * (db / dw) = 2 * 4 = 8

Ex:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10

[a] -> [+] -> [c]
[b] ->

c = a + b
dc/da = ?
dc/da = 1 + 0 = 1

dL/da = (dL / dc) * (dc / da)
dL/da = (dL / dc) * 1 = dL / dc
=> + node transfers the grad backwards, the grad is the same as previous node

Ex:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

[a] -> [*] -> [c]
[b] ->

c = a * b
dc/da = ?
dc/da = a * db/da + b * da/da = b
dc/db = a * db/db + b * da/db = a

dL/da = (dL / dc) * (dc / da) = (dL / dc) * b
dL/db = (dL / dc) * (dc / db) = (dL / dc) * a
=> grad through the * node is previous node grad times the value of the opposite node

Implementation

1. reversed topological sort

   • graph traversal in which each node v is visited only after all its dependencies are visited (for DAG only = tree)
   • https://en.wikipedia.org/wiki/Topological_sorting
   • https://www.youtube.com/watch?app=desktop&v=eL-KzMXSXXI

2. compute grad of each node, apply chain rule repetitively

   • base case = 1

1
2
3
4
5
6
7
8
9

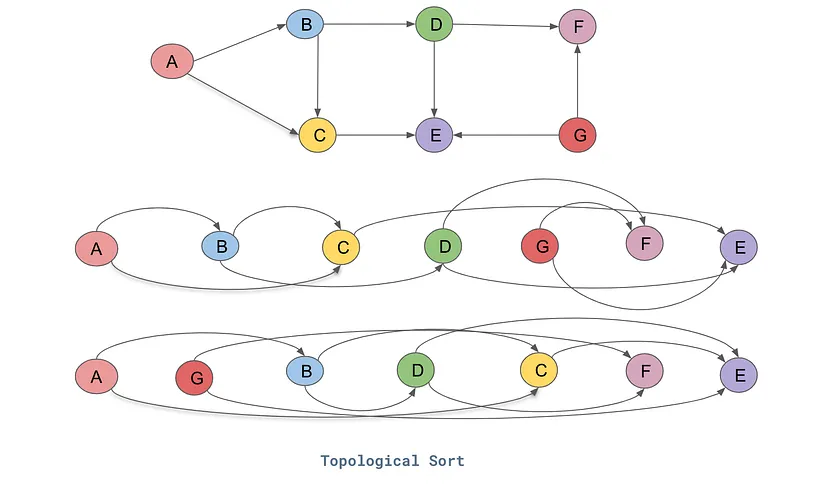
topo = []
visited = set()
def build_topo(n):
    if n not in visited: # maintain visited set of nodes
        visited.add(n)
    for child in n.children:
        build_topo() # recursion
    topo.append(n) # add parent *after* all children have been visited
build_topo(root)

Bug

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12

b = a + a
db/da = 2  != 1
if &a == &a (point to same address)

or

d = a * b
e = a + b
f = d * e

whenever reuse variable more than once
need to accumulate grad not just set it! (must init grad to 0)

https://en.wikipedia.org/wiki/Chain_rule#Multivariable_case

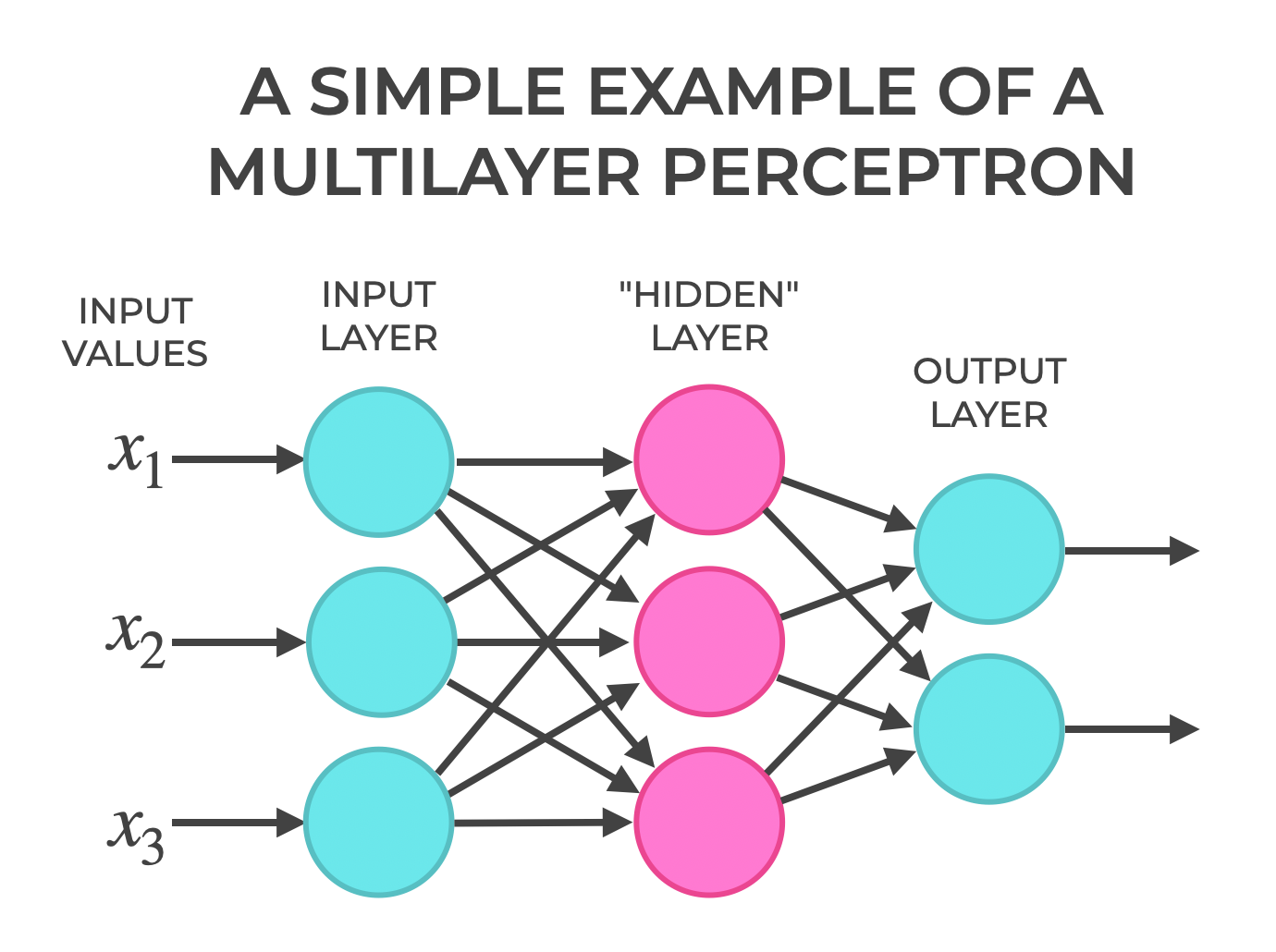
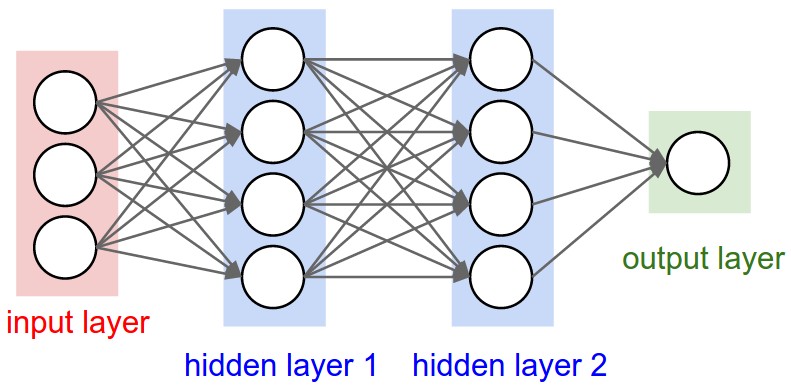
Neural networks (nnet)

• MLP (Multi Layer Perceptron) = layers of neuron (fully connected)

  • nnet of n layers = #hidden, exclude input + output layer
  • activation fct : sigmoid (logistic, tanh), relu (https://en.wikipedia.org/wiki/Activation_function)

• neuron (Perceptron) = weighted sum + bias

1
2

input = input data, weights, biases
output = loss

backprop -> iterative improve weights to min loss (train nnet):

• gradient points in direction of increasing value
• to min L, take step in direction opposite to gradient
• known as "gradient descent", optimization problem

Impl

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
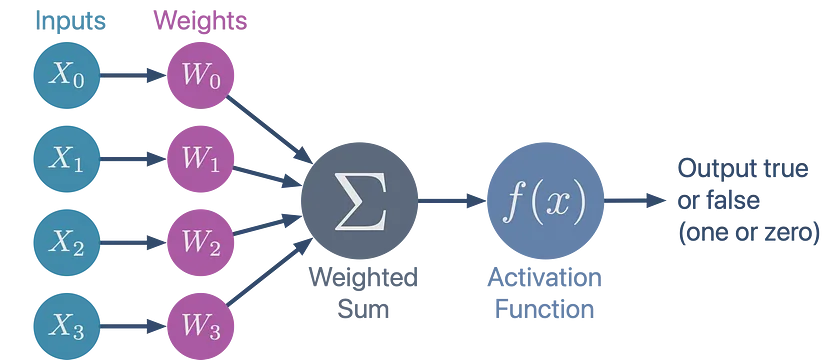
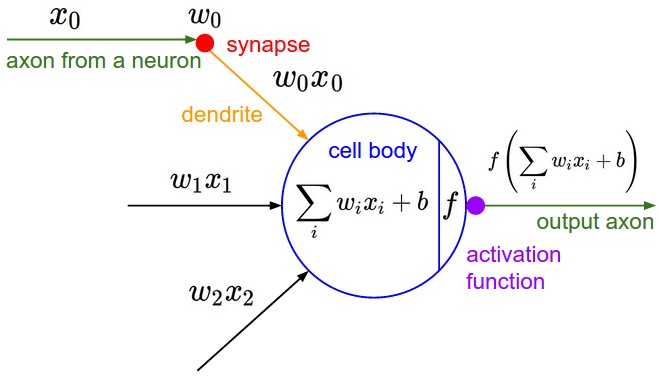
17

Neuron
    ctor: init w,b to [-1,1]
    call: Wx+b, # forward()
    parameters() list of w + b
        zip(a,b) # zip a with b, pair each element of a and b together
        sum(v, init value)
Layer = N indep Neuron
MLP = N layers
    parameters()
        flat list of all parameters (w,b)
Module
    zero_grad()
    parameters()

x = [2.0, 3.0, -1.0]
nn = MLP(3, [4,4,1])
nn(x)

train nnet with gradient descent

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17

for t in epochs
    # forward
    ypred = nn(x) 
    loss = MSE(ypred, yref)

    # flush grad
    p.zero_grad()    
        for p in nn.parameters()
            p.grad = 0.0
    # backward
    loss.backward()

    # update
    # optimizer.step()
    for p in nn.parameters()
        learning_rate = 0.01 # not too big (unstable, !converge), not too small (slow)
        p.data += learning_rate * -p.grad

• learning rate decay, shrink over time 1.0 - 0.9/100*t

Loss function

measure perf of nnet:

• MSE = sum((y - yref)^2)
• cross entropy
  • binary cross entropy
  • negative log likelihood (-log(softmax(x))), logit
• max margin loss

micrograd vs PyTorch

• similar API
• much smaller, ~200lines of python!
• scalar vs tensor = optimization

PyTorch

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

import torch
x1 = torch.Tensor([2.0]) # create tensor
x1 = x1.double() # cast (default type = f32)
x1.requires_grad = True # leaf nodes (default = no grad)
x1.shape # get dimensions
x1.dtype # get type
x2 = torch.Tensor([3.0])
x3 = torch.tanh(x1 + x2) # exec operations
x3.data.item() or x3.item() # get value (.item() returns value, strips out tensor)
x3.grad.item() # get grad
x3.backward() # run backprop

Python tricks

• __repr__ vs __str__ : str is for making it look good, repr is for making it accurate (debug)
• __rmul__ : 1 * object
• __truediv__ : a / b
• __pow__ : a^n
• format string
  • "some {.4f} value".format(var)
  • f"some {var} value"
  • "%.4f" % var
• put 2 lines on 1 : line 1; line 2
• _private_method()
• use _ as unused variable name

Includes

1
2
3
4

import math
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline #  plot immediately after running plt.plot() (jupyter notebook)

Draw graph of nodes

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

from graphviz import Digraph

def trace(root):
    nodes, edges = set(), set()
    def build(v):
        if v not in nodes:
            nodes.add(v)
            for child in v._prev:
                edges.add((child, v))
                build(child)
    build(root)
    return nodes, edges

def draw_dot(root, format='svg', rankdir='LR'):
    """
    format: png | svg | ...
    rankdir: TB (top to bottom graph) | LR (left to right)
    """
    assert rankdir in ['LR', 'TB']
    nodes, edges = trace(root)
    dot = Digraph(format=format, graph_attr={'rankdir': rankdir}) #, node_attr={'rankdir': 'TB'})

    for n in nodes:
        dot.node(name=str(id(n)), label = "{ data %.4f | grad %.4f }" % (n.data, n.grad), shape='record')
        if n._op:
            dot.node(name=str(id(n)) + n._op, label=n._op)
            dot.edge(str(id(n)) + n._op, str(id(n)))

    for n1, n2 in edges:
        dot.edge(str(id(n1)), str(id(n2)) + n2._op)

    dot.render('gout')